Quantize What Counts: More For Keys, Less For Values ☝️🔑👇🔢

TL;DR: Keys carry more information than values; consequently, key tensors require a larger quantization bit-width, smaller group sizes, and outlier mitigation (e.g., Hadamard transformation).

Abstract

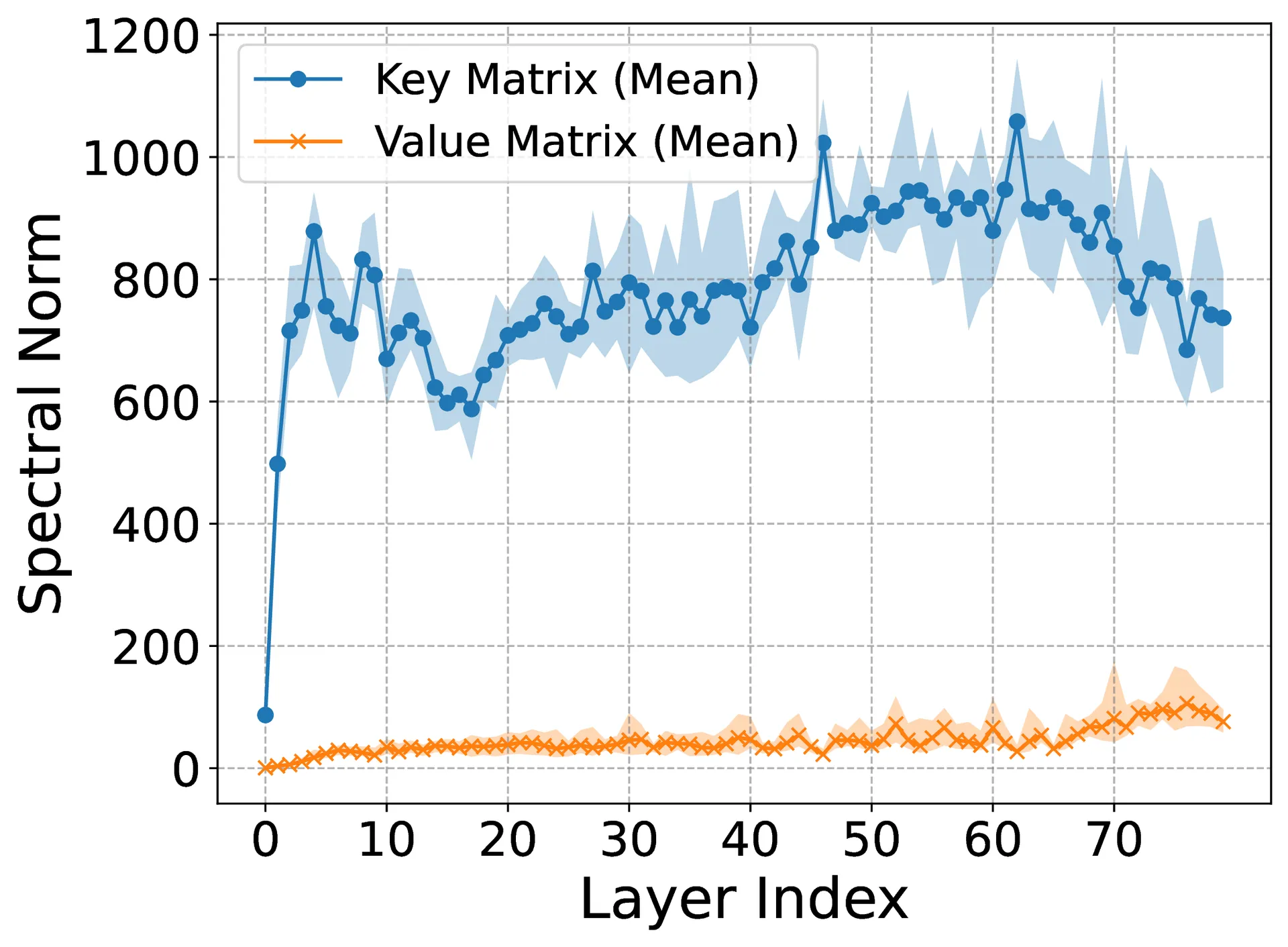
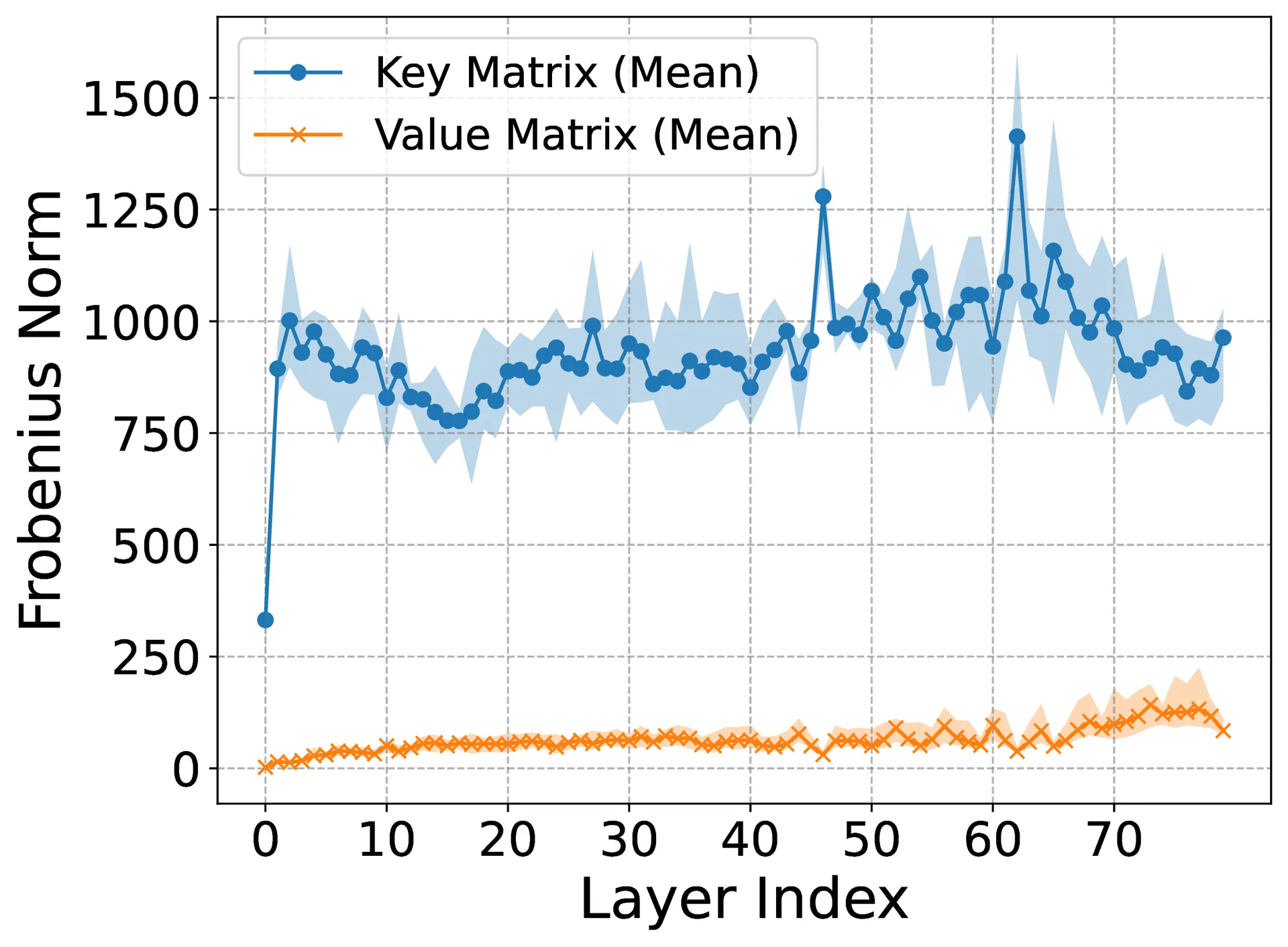
Large Language Models (LLMs) suffer inference-time memory bottlenecks dominated by the attention Key–Value (KV) cache, which scales with model size and context length. While KV-cache quantization alleviates this cost, bit allocation between keys and values is often tuned heuristically, lacking theoretical grounding and generalizability. This paper proposes two theorems that anchor mixed-precision KV quantization in the intrinsic geometry of Transformer models. First, key projections systematically have larger spectral and Frobenius norms than value matrices, implying higher information density along the key path. Second, for any given memory budget, prioritizing precision for keys over values strictly reduces quantization error and better preserves accuracy. Empirical evaluations across various prominent LLMs and benchmarks show that key-favored allocations (e.g., 4-bit keys, 2-bit values) retain up to 98.3% accuracy compared to uniform allocations (e.g., 4-bit for both), while conserving memory. These results transform bit allocation from ad hoc tuning into a theoretically grounded, geometry-driven design principle for efficient LLM inference. Source code is available at https://github.com/mohsenhariri/spectral-kv.

Theorem I. Key–Value Norm Disparity Let $\mathrm{W}^K$ and $\mathrm{W}^V$ denote the key and value projection matrices in an attention block. Then

\mathbb{E}\left[\lVert \mathrm{W}^K \rVert_{F}\right] > \mathbb{E}\left[\lVert \mathrm{W}^V \rVert_{F}\right].

Theorem II. Key–Prioritized Quantization Let $(b_K,b_V)$ denote the bit allocations for key and value caches under a uniform scalar quantizer. For any pair with $b_K > b_V$ , the expected inference accuracy is strictly higher than for the swapped allocation $(b_V,b_K)$ , provided that

\mathbb{E}\left[\lVert K \rVert_{F}^{2}\right] > \mathbb{E}\left[\lVert V \rVert_{F}^{2}\right].

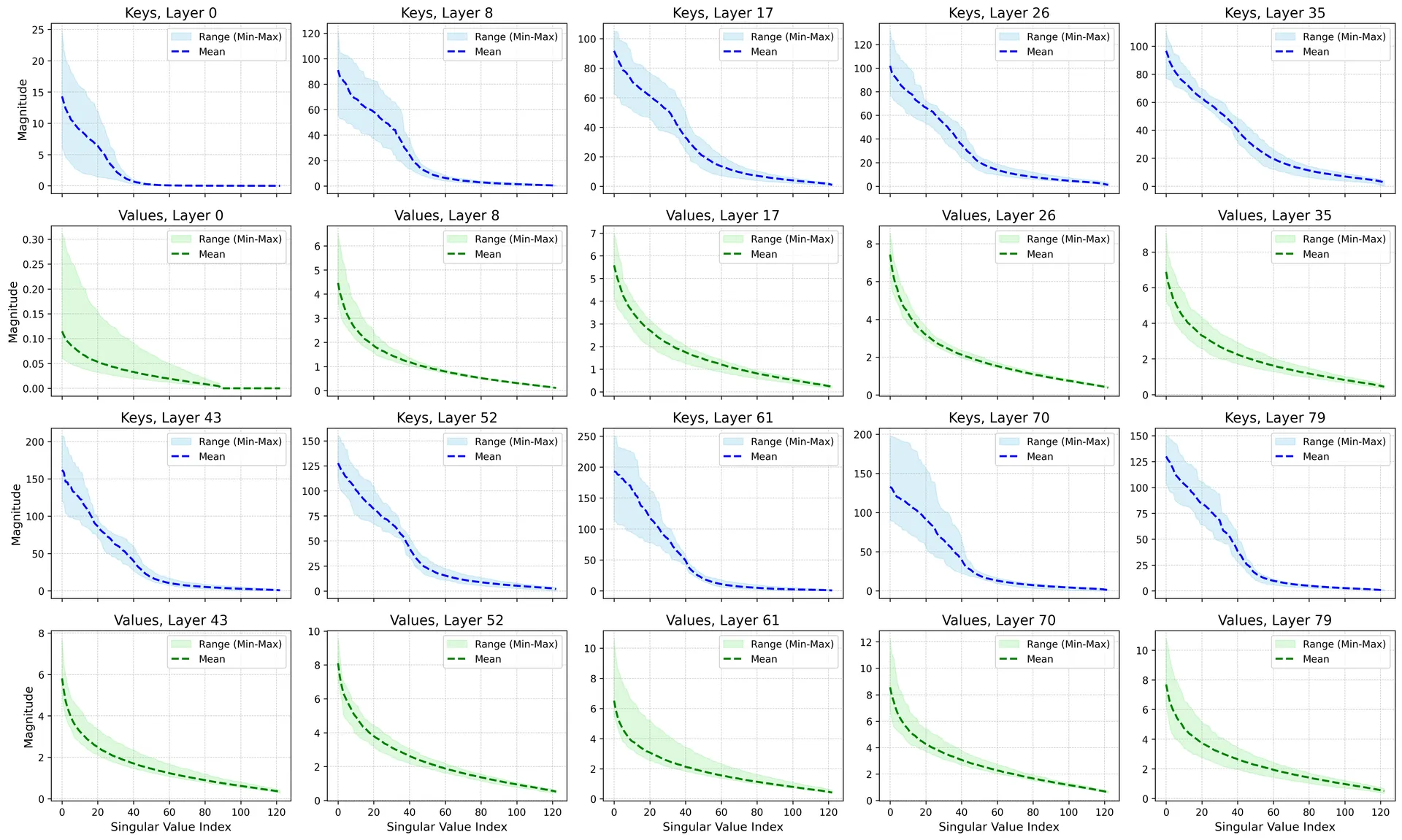
Singular value distributions over layers

Singular value spectra of key and value caches in Llama 3.3-70B on C4. The x-axis shows the singular value indices, and the y-axis shows their magnitudes. Shaded regions indicate the minimum–maximum range across attention heads within each layer, while dashed lines denote the mean at each index. Beyond the top singular value (i.e., the spectral norm), key activations consistently exhibit larger singular values than value activations across the spectrum, highlighting their greater representational capacity.

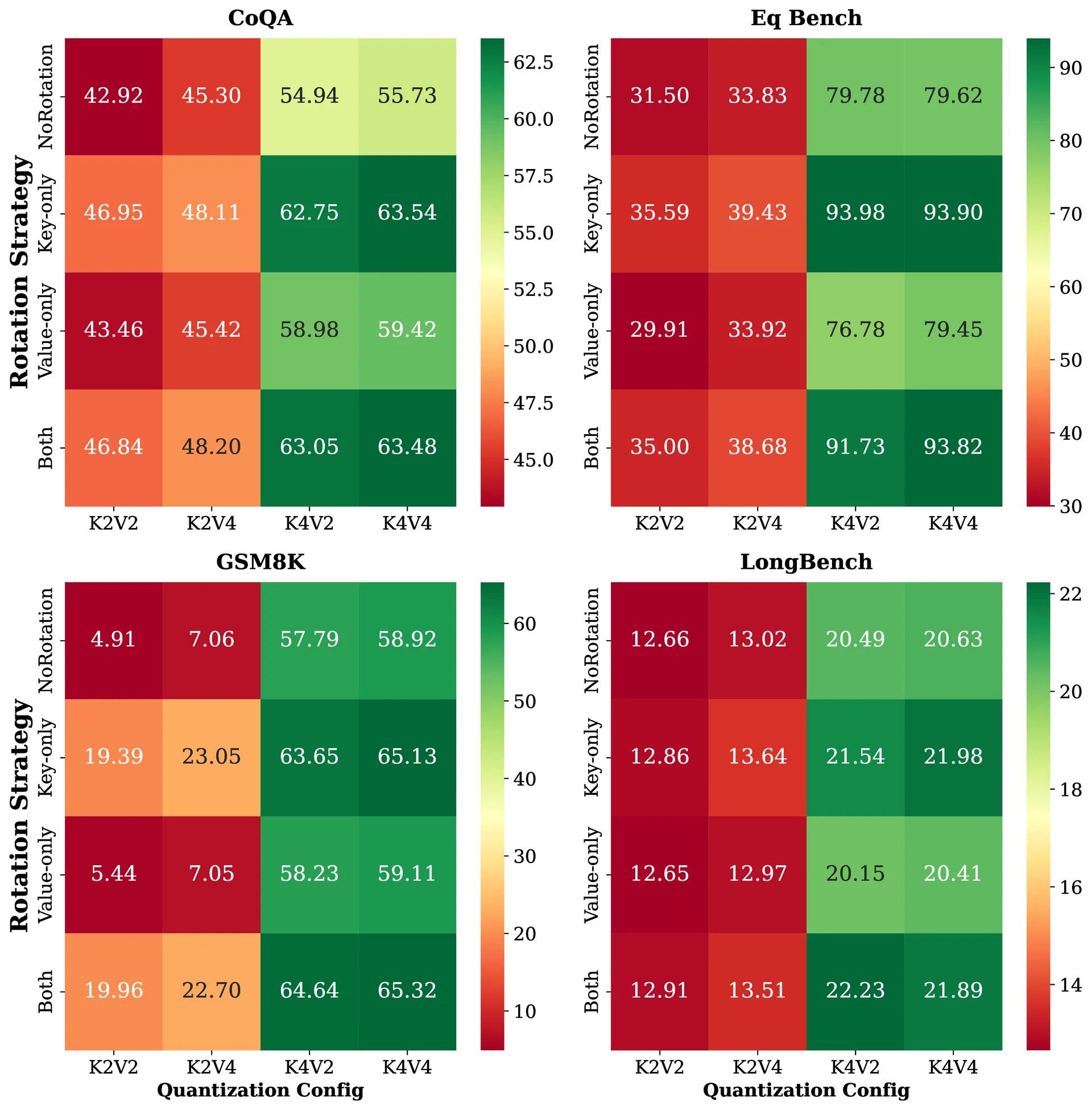
Ablations

Quantization bit-width impact

Model	Shots	K₂V₂	K₂V₄	K₄V₂	K₄V₄
Llama 3.2-1B-it	1	0.033	0.035	0.338	0.357
	8	0.031	0.031	0.289	0.369
Llama 3.1-8B-it	1	0.511	0.547	0.752	0.754
	8	0.408	0.441	0.770	0.782
Phi 4-14B	1	0.759	0.783	0.913	0.923
	8	0.771	0.815	0.927	0.931
DeepSeek R1Q-14B	1	0.772	0.775	0.865	0.867
	8	0.763	0.792	0.876	0.875

Group size impact

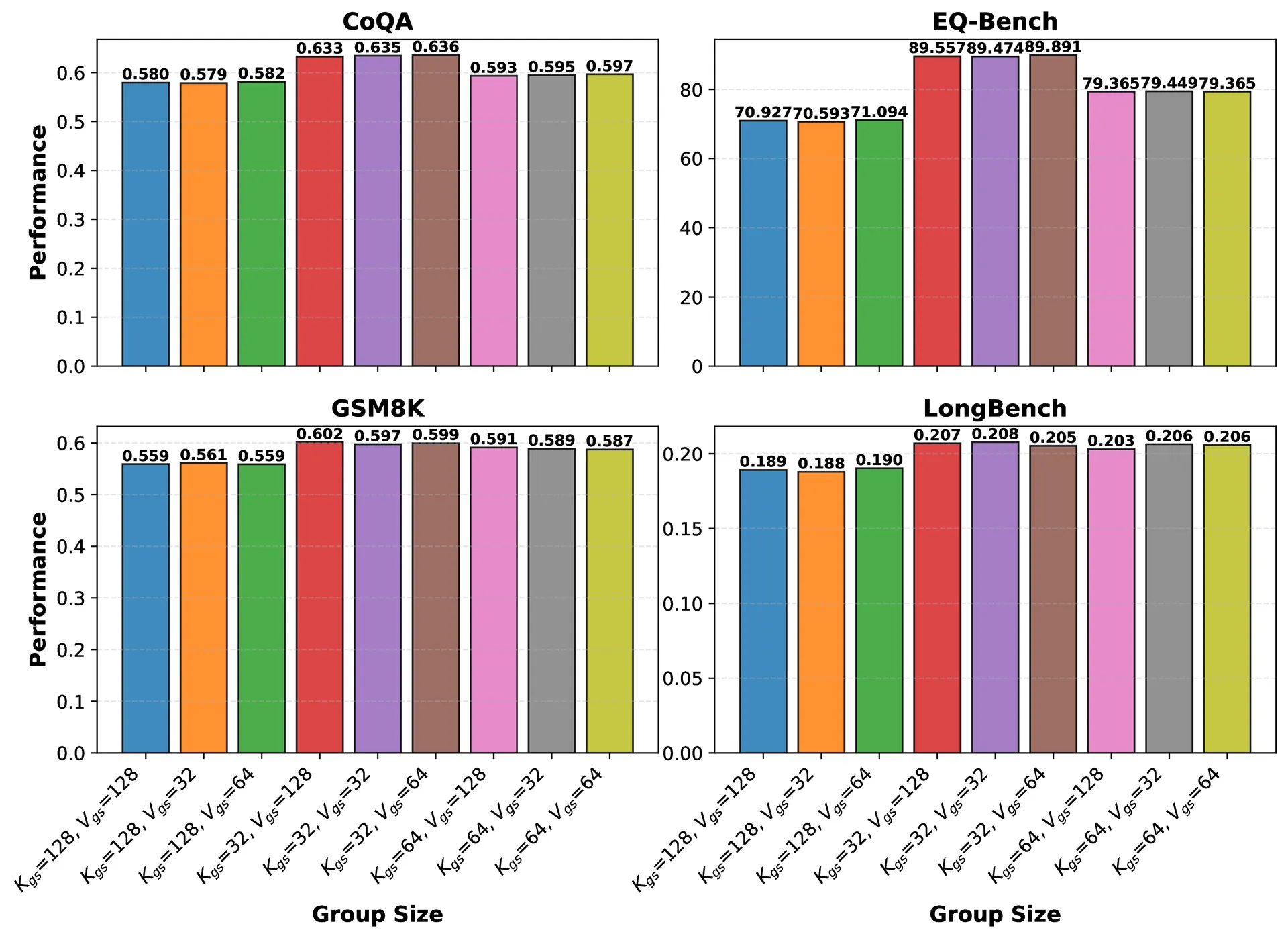
Group size comparison

Rotation impact

Rotation impact heatmap